What is Fourier Transform?
The Fourier transform, named after Joseph Fourier, is an integral transform that decomposes a signal into its constituent components and frequencies.
Introduction to the Fourier Transform
The Fourier transform (FT) is capable of decomposing a complicated waveform into a sequence of simpler elemental waves (more specifically, a weighted sum of sines and cosines). This is analogous to how a wave representing a music chord (for example, one consisting of the notes C, D, and E) can be expressed in terms of the properties of its base notes (furthermore, if we graph these notes via the Fourier transform on a frequency-versus-intensity graph, there will be visible peaks corresponding to these music notes). An original function and its transformed counterpart are collectively known as Fourier pairs, and we can use the following notation for the function:

One of the most common uses of the Fourier transform is to find the frequency range of a signal that changes over time. This form of signal processing is used in many places, such as cryptography, signal processing, oceanography, speech patterns, communications, and image recognition. Furthermore, the Fourier transform (along aside other integral transforms) can also prove to be a useful technique in solving differential equations.
A more direct application of Fourier transforms for signal decomposition would be through the Fourier series. Through Euler's formula:

We can combine sinusoids and express the Fourier series as:
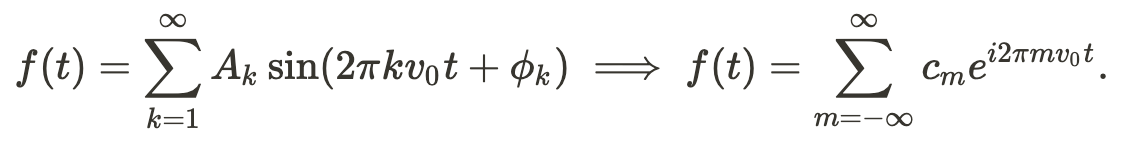
For coefficients:

For a fundamental frequency v_0 and a phase angle phi_k.
History of the Fourier Transform
The first conceptions of decomposing a periodic function into a sum of simple oscillating functions date back to Babylonian mathematics, wherein a more primitive form of expressing harmonic series was used to compute astronomical position tables, referred to as ephemerides. However, an early development towards Fourier analysis was the 1770 paper Réflexions sur la résolution algébrique des équations, wherein a method of Lagrange resolvents were used to transform cubic equations. However, the true breakthrough of harmonic analysis was in the 1807 paper Mémoire sur la propagation de la chaleur dans les corps solides by Joseph Fourier, which introduced Fourier series to model all functions by trigonometric series. **
Properties of the Fourier Transform
Fourier transform bears a variety of properties (sharing several with other similar integral transforms).
Linearity
The Fourier transform holds linearity. More precisely, if we have two Fourier pairs f(x) to F(s) and g(x) to G(s), it can be shown that the Fourier transform of the sum of f(x) scaled by some constant a and g(x) scaled by some constant b is the sum of F(s) scaled by a and G(s) scaled by b.
Shift Theorem
The Shift Theorem for Fourier transforms states that for a Fourier pair g(x) to F(s), we have that the Fourier transform of f(x-a) for some constant a is the product of F(s) and the exponential function evaluated as:

Parseval's Theorem
Parseval's Theorem states that the Fourier transform is unitary. More precisely, for a Fourier pair f(x) and F(s), that the integral of the square of f(x) is equivalent to the integral of F(s). This can be expressed as:

For the Fourier pair f(x) and F(s).
Similarity Theorem
For a Fourier pair f(x) and F(s), the Similarity Theorem states that the Fourier transform of g evaluated at the product of a constant a and x equals product of the reciprocal of the magnitude of a and G evaluated at the quotient of s and a:

Derivative Theorem
For a Fourier pair f(x) and F(s), we have that the Fourier transform of the derivative of f(x) is equal to the product of i2pi*s and F(s):

Discrete Fourier Transform
The Discrete Fourier Transform (DFT) takes a signal and find the frequency values of the signal. For a finite sequence of equally-spaced samples of a function, we can utilize the discrete Fourier Transform (DFT):
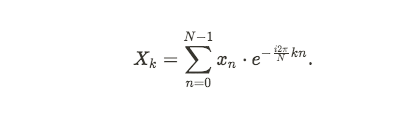
For a sequence of n complex numbers x_n.
Fast Fourier Transform (FFT)
A fast Fourier transform is an algorithm that computes the discrete Fourier transform. It quickly computes the Fourier transformations by factoring the DFT matrix into a product of factors. It reduces the computer complexity from:

where N is the data size.
This is a big difference in speed and is felt especially when the datasets grow and reach sizes of thousands or millions. When there may be a rounding error (the different between the result produced using exact arithmetic and the result using finite-precision), the FFT algorithm is actually much more accurate than the DFT.
Major fields that use FFTs are engineering, science, math (of course, and music. It was first developed by Gauss in 1805 (in one of his unpublished works) when he was trying to find the orbit of the asteroids Juno and Pallas. This was even before Fourier's research in 1822!
One of the most popular algorithms would be the Cooley-Tukey Algorithm, a divide-and-conquer algorithm that recursively breaks down a DFT into far smaller DFTs, each splitting the size of the original input by 2. This is referred to as a radix-2 decimation-in-time (DIT) FFT, and is the simplest form of the Cooley-Tukey Algorithm.
Quantum Fourier Transform (QFT)
The quantum Fourier transform is a form of the discrete Fourier transform capable of acting on quantum bits (or qubits) that can occupy a superposition of the states at values "0" and "1". For example, for a basis state x, we have that:

(There is occasionally a normalization factor of the reciprocal of the square root of N, as this also occurs in the discrete Fourier transform.)
It’s used in many algorithms — such as the quantum phase estimation algorithm for calculating the eigenvalues of an unitary operator.
The quantum Fourier transform can be either simulated on a classical computer or performed on a quantum computer (as its efficiencies are derived from the innate properties of quantum computing).
Applications of Fourier Transform
There are many applications for the Fourier transform, particularly in the fields of mathematics and physics. For example, we can evaluate these transformations on discrete datasets via the discrete Fourier transform (DFT). Moreover, we can also extend the DFT in quantum computing to define the quantum Fourier transform (QFT).
It is also used in signal processing, where engineers and scientists break down waves into their components — be it radio waves or brain waves. One example of this would be edge detection, in which Fourier transform-based filters can be applied to images to identify any borders.
It's also used in the analysis of partial differential equations.
Spectrogram Analysis
As a more concrete application of Fourier analysis, we can use the Fourier transform to create a spectrogram: a representation of a frequency spectrum through time, as represented with frequency (in hertz) on the x-axis and relative power on the y-axis. Through shifting the image, we can acquire the following result in MATLAB by analyzing the sound of a London police whistle:

As can be shown above, the graph consists of two primary beats located near the zero-frequency point due to the graph's shift (as is conventional in such spectrograms).
