What is the curse of dimensionality?
The curse of dimensionality refers to the phenomena that occur when classifying, organizing, and analyzing high dimensional data that does not occur in low dimensional spaces, specifically the issue of data sparsity and “closeness” of data.
Issues
Sparsity of data occurs when moving to higher dimensions. the volume of the space represented grows so quickly that the data cannot keep up and thus becomes sparse, as seen below. The sparsity issue is a major one for anyone whose goal has some statistical significance.
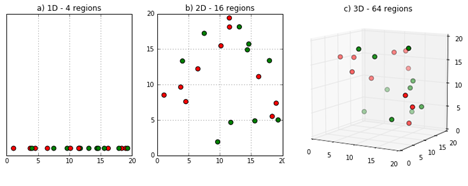
As the data space seen above moves from one dimension to two dimensions and finally to three dimensions, the given data fills less and less of the data space. In order to maintain an accurate representation of the space, the data for analysis grows exponentially.
The second issue that arises is related to sorting or classifying the data. In low dimensional spaces, data may seem very similar but the higher the dimension the further these data points may seem to be. The two wind turbines below seem very close to each other in two dimensions but separate when viewed in a third dimension. This is the same effect the curse of dimensionality has on data.

Infinite Features Requires Infinite Training
When neural networks are created they are instantiated with a certain number of features (dimensions). Each datum has individual aspects, each aspect falling somewhere along each dimension. In our fruit example we may want one feature handling color, one for weight, one for shape, etc. Each feature adds information, and if we could handle every feature possible we could tell perfectly which fruit we are considering. However, an infinite number of features requires an infinite number of training examples, eliminating the real-world usefulness of our network.
Most disconcerting, the number of training data needed increases exponentially with each added feature. Even if we only had 15 features each being one ‘yes’ or ‘no’ question about the piece fruit we are identifying, this would require a training set on the order of 21532,000 training sample.
Mitigating the Curse of Dimsionality
A careful choice of the number of dimensions (features) to be used is the prerogative of the data scientist training the network. In general the smaller the size of the training set, the fewer features she should use. She must keep in mind that each features increases the data set requirement exponentially.
